FP7 Marie Curie Re-Integration Grant 228389
interactive particle representation model
When the time scale of the mean deformation is large compared to that of the turbulence, the non-linear turbulence-turbulence interactions become important in the governing field equations. In the context of the PRM, these non-linear processes should be represented by particle-particle interactions. As in the case of the one point field equations, the non-linear processes cannot be evaluated directly and modeling is required. By doing so, the linear PRM version for the solution of RDT is extended to what we have termed the Interacting Particle Representation Method (IPRM), which takes into account the non-linear effects. Due to the introduction of modeling, the emulation of the field equations by the IPRM is no longer exact, which was the case for the PRM emulation of RDT. The basic idea behind the IPRM is quite simple. The overall effect of the background particle-particle interactions on any given particle is modeled in two parts. The first part which we call the effective gradient model, assumes that the background particle-particle interactions provide a gradient acting on the particles in addition to the mean deformation rate. The assumption is that the effective deformation rate can be expressed in terms of the mean deformation rate and statistics based on the particle ensemble, thus providing closure. The second part of the particle-particle interaction model accounts for rotational effects. Mean rotation acting on the particles tends to produce rotational randomization of the V vectors around the n vectors. Effective rotation due to particle-particle interactions should also induce a similar randomization effect. It has turned out that good results are obtained, when this slow rotational randomization effect is modeled explicitly. Different models for the effective eddy deformation tensor are possible. Here we report one such model, that we have found to produce excellent results for irrotational mean strain and good results for homogeneous shear and the elliptic stream-line flows. Direct numerical simulations show that under weak strain the structure dimensionality, D, remains considerably more isotropic than do the Reynolds stresses, R. Hence, we modify the basic equations for the evolution of the particle properties to account for these effects. By doing so, the linear PRM version for the solution of RDT was extended to what we have termed, in this project, the Interacting Particle Representation Method (IPRM), which takes into account the non-linear effects. Due to the introduction of modeling, the emulation of the field equations by the IPRM is no longer exact, which was the case for the PRM emulation of RDT. As it was concluded with a relatively simple model for the non-linear turbulence-turbulence interactions, the IPRM is able to handle quite successfully a surprising wide range of flows (see Figs). Some of these flows involve paradoxical effects and the fact that the IPRM is able to reproduce them suggests that the model captures a significant part of the underlying physics. In this sense, the IPRM is a viscoelastic structure-based model that bridges successfully RDT with k-ε theory.
|
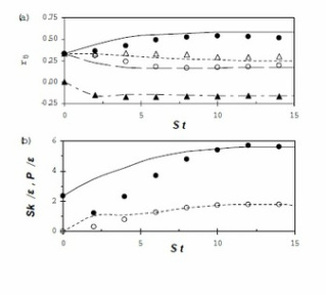
Fig 1. Comparison of IPRM predictions (lines) with DNS (symbols)for homogeneous shear flow with initial Sq^2/ε=2.36. Evolution of (a) Reynolds stresses: component 11 (continuous, solid circles), 22 (long dashed, open circles), 33 (short dashed, open triangles), 12 (dotted dashed, solid triangles). (b) Evolution of the non-dimensional parameters Sk/ε (continuous, solid circles) and P/ε (dashed, open circles). |
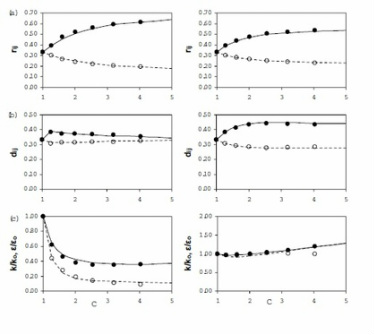
Fig 2. Comparison of IPRM predictions (lines) with DNS (symbols) for axisymmetric contraction with Sq^2/ε = 1.1 (LHS) and Sq^2/ε = 11.1 (RHS). Evolution of (a) Reynolds stresses, (b) dimensionality: component 11 (continuous, solid circles), components 22 and 33 (dashed, open circles). (c) Evolution of the normalized turbulent kinetic energy (continuous, solid circles) and dissipation rate (dashed, open circles).
|
|
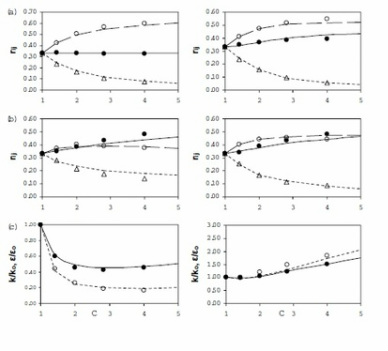
Fig 3. Comparison of IPRM predictions (lines) with DNS (symbols) for axisymmetric expansion with Sq^2/ε = 0.82 (LHS) and Sq^2/ε = 8.2 (RHS). Evolution of (a) Reynolds stresses, (b) dimensionality: component 11 (continuous, solid circles), components 22 and 33 (dashed, open circles). (c) Evolution of the normalized turbulent kinetic energy (continuous, solid circles) and dissipation rate (dashed, open circles). |
Fig 4. Comparison of IPRM predictions (lines) with DNS (symbols) for plane strain flow with Sq^2/ε = 1.0 (LHS) and Sq^2/ε = 8.0 (RHS). Evolution of (a) Reynolds stress, (b) dimensionality: component 11 (continuous, solid circles), 22 (long dashed, open circles) and 33 (short dashed, open triangles). (c) Evolution of the normalized turbulent kinetic energy (continuous, solid circles) and dissipation rate (dashed, open circles).
|