FP7 Marie Curie Re-Integration Grant 228389
particle representation of the RDT
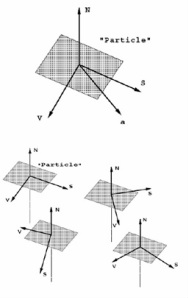
An elegant way to solve numerically the RDT systems is the Particle Representation Model (PRM) introduced by Kassinos and Reynolds (1994, 1996, 1999). This is a set of equations for the evolution of the properties of a hypothetical particle. The basic idea is to follow the evolution of an ensemble of particles, determine its statistics and use these as the model for the one point statistics of an evolving field. The equations emulate the exact equations for the evolution of the field, especially the one-point statistics. The key innovation in the present PRM approach lies in the recognition that the linearity of the RDT governing equations makes it possible to emulate exactly the RDT for homogeneous turbulence using a PRM without any modeling assumptions. The non-local pressure effects can be evaluated within the framework of the PRM, thus providing closure. This is unlike traditional particle representation approaches employed by the combustion community. In these traditional particle representations, usually in the form of PDFs, modeling assumptions are introduced at some level, to account for the effects of the fluctuating pressure gradient and molecular viscosity on the evolution of the particle velocity. One can take moments of the governing stochastic evolution equations to form equations for one-point statistics, like the Reynolds stresses. To each assumed stochastic model corresponds an equivalent one-point Reynolds Stress Transport (RST) model. Hence, it is common in PDF models to assume a stochastic model that will produce one of the standard RST models, but in this way modeling is introduced where it is not needed i.e. in matching RDT. Here we present the basic idea behind the PRM for the exact emulation of the RDT of homogeneous turbulence. We start with a discussion of the properties assigned to each of the hypothetical particles and a geometrical interpretation of the particles. The assigned properties are V velocity vector, W vorticity vector, S stream function vector, N gradient vector and P pressure. These hypothetical particles represent an idealized building block for the turbulence structure. Each particle corresponds to a plane of independence. Based on the one-to-one correspondence of the properties of the particles with the respective field quantities, the Reynolds stress Rij = uiuj, are exactly calculated by averaging the corresponding particle properties. The idea in the cluster averaged method is to do the averaging in two steps, the first step being done analytically. First an averaging is done over particles that have the same n(t) followed by an averaging over all particles with different n(t). These particle clusters correspond to 1D-2C vortical flows (vortex sheets) as shown in Figure.
Fig. Hypothetical “particle” and cluster
of particles forming an 1D - 2C flow.
Fig. Hypothetical “particle” and cluster
of particles forming an 1D - 2C flow.
